Skip to content

Binning Data

When dealing with continuous numeric data, it is often helpful to bin the data into multiple buckets for further analysis. There are several different terms for binning including bucketing, discrete binning, discretization or quantization.

One of the most common instances of binning is done behind the scenes for you when creating a histogram. The histogram below of customer sales data, shows how a continuous set of sales numbers can be divided into discrete bins (for example: $60,000 - $70,000) and then used to group and count account instances.

Binning Data

Pandas cut

Pandas cut and qcut info is taken from pbpython

Documentation

cut_labels_4 = ['silver', 'gold', 'platinum', 'diamond']
cut_bins = [0, 70000, 100000, 130000, 200000]
df['cut_ex1'] = pd.cut(df['ext price'], bins=cut_bins, labels=cut_labels_4)
account number name ext price cut_ex1
141962 Herman LLC 63626.03 silver
146832 Kiehn-Spinka 99608.77 gold
163416 Purdy-Kunde 77898.21 gold
218895 Kulas Inc 137351.96 diamond
239344 Stokes LLC 91535.92 gold

Pandas qcut

Documentation

The pandas documentation describes qcut as a “Quantile-based discretization function.” This basically means that qcut tries to divide up the underlying data into equal sized bins. The function defines the bins using percentiles based on the distribution of the data, not the actual numeric edges of the bins.

The simplest use of qcut is to define the number of quantiles and let pandas figure out how to divide up the data. In the example below, we tell pandas to create 4 equal sized groupings of the data. 

df['quantile_ex_1'] = pd.qcut(df['ext price'], q=4)
df['quantile_ex_2'] = pd.qcut(df['ext price'], q=10, precision=0)

df.head()

account number name ext price cut_ex1 quantile_ex_2
141962 Herman LLC 63626.03 (55733.049000000006, 89137.708] (55732.0, 76471.0]
146832 Kiehn-Spinka 99608.77 (89137.708, 100271.535] (95908.0, 100272.0]
163416 Purdy-Kunde 77898.21 (55733.049000000006, 89137.708] (76471.0, 87168.0]
218895 Kulas Inc 137351.96 (110132.552, 184793.7] (124778.0, 184794.0]
239344 Stokes LLC 91535.92 (89137.708, 100271.535] (90686.0, 95908.0]

Fisher-Jenks Algorithm

Documentation

What we are trying to do is identify natural groupings of numbers that are “close” together while also maximizing the distance between the other groupings. Fisher developed a clustering algorithm that does this with 1 dimensional data (essentially a single list of numbers). In many ways it is similar to k-means clustering but is ultimately a simpler and faster algorithm because it only works on 1 dimensional data. Like k-means, you do need to specify the number of clusters. Therefore domain knowledge and understanding of the data are still essential to using this effectively.

The algorithm uses an iterative approach to find the best groupings of numbers based on how close they are together (based on variance from the group’s mean) while also trying to ensure the different groupings are as distinct as possible (by maximizing the group’s variance between groups).

import pandas as pd
import jenkspy

sales = {
    'account': [
        'Jones Inc', 'Alpha Co', 'Blue Inc', 'Super Star Inc', 'Wamo',
        'Next Gen', 'Giga Co', 'IniTech', 'Beta LLC'
    ],
    'Total': [1500, 2100, 50, 20, 75, 1100, 950, 1300, 1400]
}
df = pd.DataFrame(sales)
df.sort_values(by='Total')
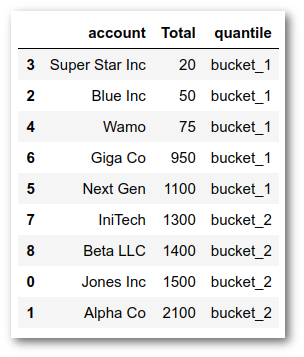
which yields this dataframe

dataframe

In order to illustrate how natural breaks are found, we can start by contrasting it with how quantiles are determined. For example, what happens if we try to use pd.qcut with 2 quantiles? Will that give us a similar result? 

df['quantile'] = pd.qcut(df['Total'], q=2, labels=['bucket_1', 'bucket_2'])
dataframe

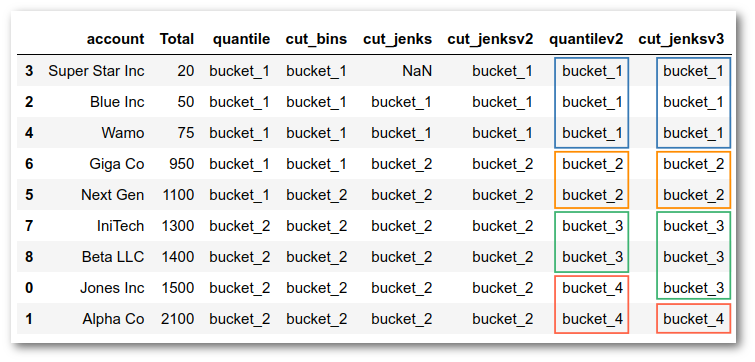
Just to get one more example, we can see what 4 buckets would look like with natural breaks and with a quantile cut approach: 

df['quantilev2'] = pd.qcut(
    df['Total'], q=4, labels=['bucket_1', 'bucket_2', 'bucket_3', 'bucket_4'])

df['cut_jenksv3'] = pd.cut(
    df['Total'],
    bins=jenkspy.jenks_breaks(df['Total'], nb_class=4),
    labels=['bucket_1', 'bucket_2', 'bucket_3', 'bucket_4'],
    include_lowest=True)

df.sort_values(by='Total')
jenks